Применение Perl для построения и преобразования гистограмм сигналов (часть 3). М.В. Смирнов.

АННОТАЦИЯ: Третья статья серии "Моделирование методов цифровой обработки сигналов на языке Perl" посвящена реализации алгоритмов для построения и преобразования гистограмм сигналов и статистических распределений. Описание сигналов с помощью гистограмм один из эффективных методов анализа и находит широкое применение во многих областях познания. Perl позволяет получить интересные решения для построения гистограмм с помощью упорядоченных массивов и хэшей - ассоциативных массивов. В предыдущих статьях серии дано введение в математический пакет Math::FFT (Fast Fourier Transform) архива свободных программных ресурсов CPAN (Comprehensive Perl Archive Network) и представлены методы цифровой фильтрации сигналов с помощью подпрограмм этого пакета. Остальные статьи цикла посвящены моделированию и визуализации голограмм Фурье двумерных сигналов.

1. Массивы и хэши в задаче подсчета объектов

Каждый раз, когда возникает задача подсчета различных объектов, стоит воспользоваться хэшем [1]. Вместе с тем, во многих численных задачах бывает проще использовать массивы, которые представляют собой упорядоченные скаляры с целочисленными индексами. Целочисленные индексы массивов позволяют ссылаться на скаляры в соответствии с некоторым упорядоченным перебором целых чисел. Рассмотрим пример построения гистограммы измерений температуры воздуха. Диапазон изменения температуры воздуха ограничим значениями минус 50 и плюс 50 градусов по Цельсию. Собственно процедура построения гистограммы сводится к инкрементации массива гистограммы @TERMO по целочисленной ссылке $t: @TERMO = (0) x 100; foreach(@DATA){ $t = int($_) + 50; $TERMO[$t]++; }, где @DATA массив значений температуры за шесть месяцев (день, ночь) по данным сборника прогнозов погоды[2]. График полученной гистограммы показан на рис.1.

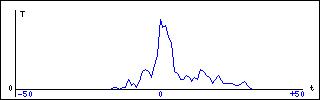
Рис. 1. Гистограмма температур воздуха.
Применение массивов усложнится, если в качестве объектов будут текстовые строки "Ясно", "Малооблачно", "Облачно", "Пасмурно с просветами", "Пасмурно". В этом случае, значительно эффективнее использовать хэши, получившие так же название ассоциативных массивов. Если в обычных массивах используются числовые индексы, то в хэшах используются не индексы, а ключи, которые всегда являются строковыми. В качестве примера рассмотрим задачу оценки статистики повторения слов, которая актуальна для поисковых систем. Поставлена следующая задача: подсчитать частоту повторения слов в произвольном тексте.

Решение будет включать следующие этапы:
- удаление всех символов, которые не являются символами кириллицы или латиницы;
- перевод всех символов текста к нижнему регистру;
- выполнение подсчета и сортировки слов, исключая предлоги, которые находятся в массиве @PRE.

Исходный текст содержится в строковой переменной $text. Код программы: @PRE=("к","с","на","о","из","то","и", "с", "в", "а", "к"); foreach(@PRE){ $nowords{$_}=1; } $text =~ s/[^0-9a-zA-Zа-яА-Я]+/ /gs; $text = lc($text); $text = toLowerCyr($text); @histo=split (/ /,$text); foreach(@histo) { if($nowords{$_}) { next; } $HS{$_}++; } $i=1; foreach (sort { $HS{$b} <=> $HS{$a} } keys(%HS)) { print "i=$i $_ => $HS{$_}\n"; if($HS{$_} < 2){ last;} $i++; } sub toLowerCyr{ my $txt = shift; $txt =~ tr{\xC0-\xDF}{\xE0-\xFF}; return $txt; } Вывод на печать представляет собой гистограмму частот появления слов в тексте: i=1 подарок => 7 i=2 если => 5 i=3 или => 4 i=4 сувениры => 4 i=5 нужен => 3 i=6 вам => 3 i=7 лазерной => 2 i=8 графикой => 2 i=9 для => 2 i=10 подарки => 2 i=11 сувениров => 1. Подпрограмма toLowerCyr() используется для приведения символов кириллицы к нижнему регистру. Конструкция sort{$HS{$b} <=> $HS{$a}}, в последнем цикле foreach(), обеспечивает сортировку гистограммы %HS по убыванию. Выход из этого цикла происходит при появлении второго значения гистограммы равного 1, и осуществляется с помощью команды last.

2. Описание сигналов с помощью гистограмм первого и второго порядка

К построению гистограмм сигналов прибегают всякий раз, когда возникает необходимость оценить закон распределения сигнала как случайной величины. Если объектами подсчета являются целочисленные значения цифрового сигнала, после его преобразования в аналого-цифровом преобразователе, то для построения гистограмм вполне оправдано применение обычных массивов. В качестве примера рассмотрим прямоугольный видео импульс (рис.2), искаженный передаточной функцией приемника видеосигнала и шумами:

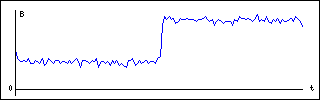
Рис. 2. График видеосигнала.
Для построения гистограммы видеосигнала, представленного на рис.2, реализация кода проста и очевидна: $M = 256; @HV = (0) x $M; for($i=0;$i<$N; $i++){ $m = $video[$i]; $HV[$m]++; }, где $N - размерность последовательности значений видеосигнала, @HV - массив гистограммы. Результат построения гистограммы показан на рис.3:

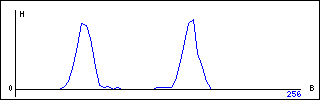
Рис. 3. Гистограмма видеосигнала.
Если же необходимо построить гистограмму видеосигнала с одновременной сортировкой значений, например, по убыванию, то код с использованием массивов будет значительно сложнее. В этом случае эффективнее использовать хэши: for($i=0;$i<$N;$i++){ $m = $video[$i]; $HSV{$m}++; } foreach (sort { $HSV{$b} <=> $HSV{$a} } keys(%HSV)) { print "$_ => $HSV{$_}\n"; }, где хэш %HSV содержит значения гистограммы. Вывод на печать представляет собой гистограмму значений видеосигнала, упорядоченных по убыванию: 39 => 63 15 => 61 16 => 59 40 => 45 38 => 44 14 => 43 17 => 37 41 => 30 18 => 23 42 => 22 37 => 17 36 => 14 13 => 12 43 => 9 19 => 8 12 => 7 35 => 3 44 => 3 31 => 2 34 => 2 20 => 2 22 => 2 11 => 1 26 => 1 23 => 1 33 => 1. Наряду с рассмотренными статистиками, которые являются функциями одной переменной, большое значение приобрели гистограммы второго порядка. Эти гистограммы оказались наиболее востребованными в задачах анализа и синтеза текстурных изображений [3], то есть двумерных сигналов. Гистограммы второго порядка, показывают условную вероятность совместного появления предшествующего и последующего значения сигналов. Оценить значимость описания сигналов, с помощью гистограмм второго порядка, можно на примере одномерных генераторов шума, которые обычно используются при моделировании цифровых систем передачи данных. Генерирование равномерно распределенного шума в Perl осуществляется с помощью встроенной функции rand(), которая используется в подпрограмме smgauss() для создания Гауссова нормального шума. Код программы, для построения гистограммы второго порядка показан ниже: $NB=10000; $M=32; for($j=0;$j<$M; $j++){ for($i=0;$i<$M; $i++){ $w[$i][$j]=0; }} for($t=0;$t<$NB; $t++){ $b[$t]=int($M*(&smgauss($t) + 1)/2); } for($t=1;$t<$NB; $t++){ $i=$b[$t-1]; $j=$b[$t]; $w[$i][$j]++; } sub smgauss{ local(*J)=@_; $U=0; $AN12=12; for($i=$J;$i<$J+$AN12; $i++){ $x=2*(rand(10)/10 - .5); $U +=$x; } return $U/($AN12-1); } Результирующая гистограмма содержится в двумерном массиве @w. Размерность выборки нормального шума задана значением $NB, а значение $M определяет число уровней квантования. Результат построения гистограммы второго порядка представлен на рис.4:

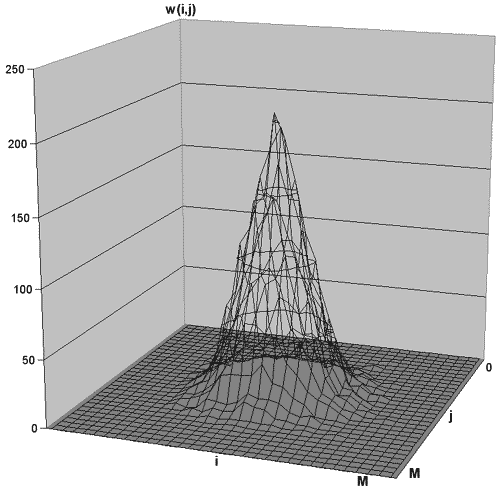
Рис. 4. Гистограмма второго порядка нормального шума.

3. Методы преобразования гистограмм сигналов при решении практических задач

Наиболее простой, и быстрый метод преобразования видеосигналов состоит в амплитудной коррекции сигнала[3]. Амплитудная коррекция приводит к изменению гистограммы сигнала. Функция преобразования, нелинейная в общем случае, задается в виде таблицы, что позволяет при обращении к этой таблице по адресу входного сигнала, получить преобразованный выходной сигнал. Эта процедура оказалась наиболее востребованной в графических программах подобных Adobe Photoshop. Рассмотрим пример преобразования видеосигнала на рис.2 в соответствии с таблицей преобразования, график значений которой показан на рис.5:

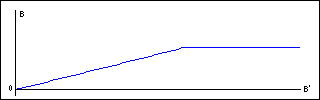
Рис. 5. Функция преобразования видеосигнала.
Применение такой корректирующей функции обычно требуется при ограничении динамического диапазона сигнала с одновременным подавлением шумовых выбросов. Результат применения амплитудной коррекции показан на рис.6:

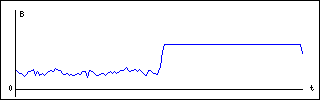
Рис. 6. Результат амплитудной коррекции видеосигнала.
Фрагмент программы, для реализации амплитудной коррекции показан ниже: $Lm = $Bmax - $rms; for ($i=0; $i<$M; $i++) { if($i >= $Lm){ $in = $Lm; }else{ $in = $i;} $table[$i]=$in; } . . . . . . . . . for($i=0;$i<$N; $i++){ $in = $video[$i]; $out[$i] = $table[$in]; } где $M - число уровней квантования, $Bmax - максимальное значение видеосигнала, $rms - стандартное отклонение шума. Значения корректирующей функции сохраняются в массиве @table, входной сигнал задается в массиве @video, а выходной сохраняется в массиве @out.

Другой метод преобразования получил название метода моды[4] и основывается на определении пиков (мод) в гистограмме сигнала. Разбиение сигнала на участки осуществляется выбором порога по провалам значений гистограммы между модами. На рис.7 показана оптическая интерференционная картина:

Рис. 7. Интерференционная картина.
Для восстановления фазы, анализируемой оптической системы, обычно используется метод расчета центров интерференционных полос. Задачу для программирования сформулируем следующим образом:
- построить гистограмму видеосигнала интерференционной картины;
- определить порог для селекции полос интерференции;
- преобразовать (контрастировать) видеосигнал в соответствии с выбранным порогом.

Фрагмент программы для расчета гистограммы показан ниже: $M = 256; @histo = (0) x $M; for($y=0;$y<$height; $y++){ for($x=0;$x<$width; $x++){ $m = $video[$y][$x]; $histo[$m]++; }} где $height и $width - высота и ширина цифрового изображения интерферограммы, соответственно. На рис.8 показана гистограмма @histo видеосигнала @video интерференционной картины на рис.7.

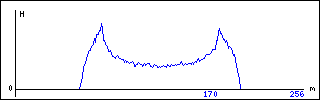
Рис. 8. Гистограмма видеосигнала интерференционной картины.
Пороговое значение $thres для контрастирования полос интерференции оценим как $thres = $average + $rms, где $average - среднее видеосигнала, $rms - стандартное отклонение, $M - уровни квантования. Фрагмент программы для оценки порога контрастирования видеосигнала показан ниже: $sum = 0; for($m=0;$m<$M; $m++){ $sum += $m*$histo[$m]; } $average = $sum/($height*$width); $sum2 = 0; for($m=0;$m<$M; $m++){ $sum2 += $histo[$m]*($m - $average)**2; } $rms = sqrt($sum2/($height*$width)); $thres = int($average + $rms); print "\$average=$average \$rms=$rms \$thres=$thres\n"; for($y=0;$y<$height; $y++){ for($x=0;$x<$width; $x++){ if($video[$y][$x] > $thres){ $out[$y][$x] = 255; }else{ $out[$y][$x] = 0; } }} Контрастирование видеосигнала выполняется в процессе сравнения с порогом, а именно, выходным данным @out присваивается значение 255 при превышении порога $thres, и значение 0 противном случае. На печать выводится расчет значений параметров: $average=127.4, $rms=43.1 и $thres=170, которые определены по гистограмме видеосигнала. Результат контрастирования интерференционной картины показан на рис.9:

Рис. 9. Результат контрастирования интерференционной картины.
Центры интерференционных полос рассчитываются по половине ширины видеосигнала полос, после выполнения процедуры контрастирования.

4. Выводы

Применение Perl целесообразно при описании сигналов и процессов с помощью гистограмм первого и второго порядка. Показаны возможности Perl в задачах моделирования методов оценивания и преобразования цифровых данных по их гистограммам. Представлены примеры, показывающие в каких случаях лучше использовать обычные массивы, а в каких эффективнее применение хэшей.

ЛИТЕРАТУРА: [1] Библиотека программиста Perl - Т.Кристиансен, Н.Торкингтон. [2] Сборник прогнозов погоды - http://thermo.karelia.ru/. [3] Цифровая обработка изображений - Э.Прэтт. [4] Распознавание и обработка изображений - А.Розенфельд.